Тема 1. Просторові об’єкти, шкали вимірювань та системи координат

Картографічні проекції – математично визначене відображення поверхні еліпсоїда або кулі (глобуса) на площину карти.

Проекції – не абсолютно точне представлення географічного простору, оскільки еліпсоїд неможливо спроектувати на площину. Кожна створює свій набір типів і величин спотворень на карті. Важливі характеристики карт, які повинні зберігатися для точних аналітичних операцій, часто визначають вибір тієї чи іншої проекції.

Картографічні проекції, які використовують для зображення земного еліпсоїда на площині карти, класифікують за такими ознаками:

1.                 Характер спотворення;

2.                 Вид допоміжної поверхні;

3.                 Орієнтування допоміжної поверхні;

4.                 Вид нормальної картографічної сітки;

5.                 Спосіб отримання та особливості користування.

Ми зупинимось тільки на основних класифікаціях.

За характером спотворень картографічні проекції поділяють на (рис. 1):

ü   Конформні або рівнокутні проекції (англ. conformal projections, orthomorphic projections), які не мають спотворень кутів і напрямів, значно спотворюються площі.

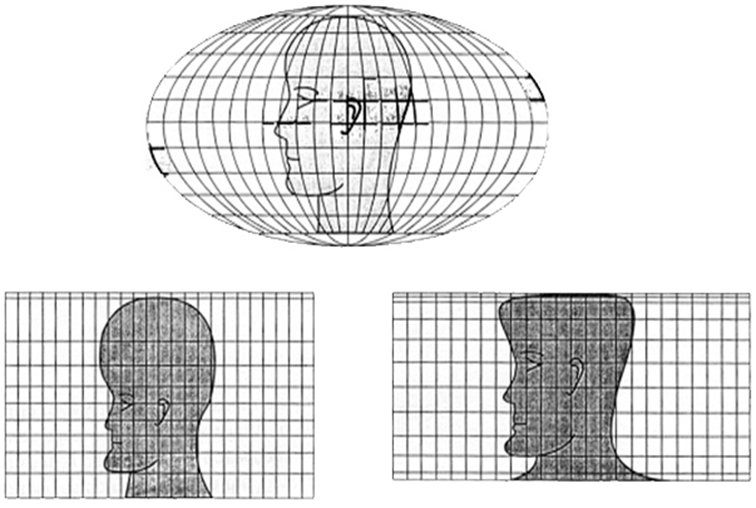
Рис. 1. Поділ проекцій за характером спотворень: а – точна форма (проекція Молвейде), б – точна площа (проекція Робінсона), в – точний напрямок (проекція Меркатора)

ü   Рівновеликі проекції (англ. equivalent projections, equal-area projections, authalic projections), які не містять спотворень площ, але спотворюються кути і площі. напрями

ü   Рівнопроміжні або еквідистантні проекції (англ. equidistant projections), які зберігають без спотворень якийсь один з напрямків (меридіани або паралелі), а спотворення кутів і площ врівноважене.

Довільні проекції (англ. arbitrary projections, compromise map projections), у яких тією чи іншою мірою містяться спотворення кутів і площ

За способом створення (за видом допоміжної поверхні на яку проектують земний еліпсоїд) вирізняються чотири сім’ї картографічних проекцій, зокрема сім’ї (рис. 2):

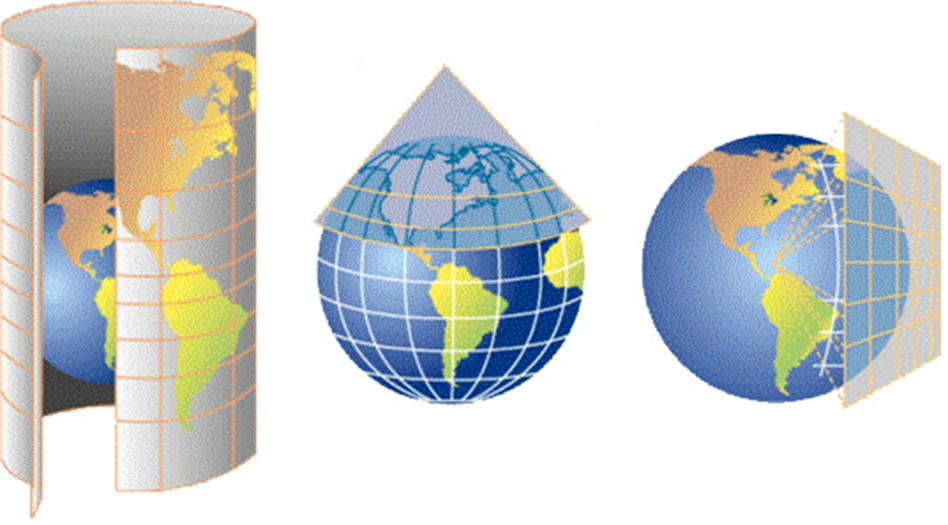
Рис. 2. Поділ проекцій за способом створення: а – циліндричні, б – конічні,
в – азимутальні

ü   циліндричних (англ. cylindrical). В циліндричний поверхня еліпсоїда переносяться на січну поверхню дотичного до неї або січного її циліндра. Після цієї операції циліндр розрізається по твірній та розгортається на площину.

ü   конічних (англ. conical). В конічних проекціях поверхня еліпсоїда переноситься на бічну поверхню дотичного до неї або січної її конуса, а потім останній розрізається по твірній та розгортається в площину.

ü   азимутальних (англ. azimuthal) проекцій. В азимутальних проекціях поверхню еліпсоїда переносять на дотичну до неї або на її січну площину.

Залежно від положення сферичних координат (за орієнтуванням допоміжної поверхні відносно полярної осі або екватора еліпсоїда) картографічні проекції поділяють на:

1.     нормальні проекції (англ. normal projections, normal aspect (or case) of a map projections), у яких вісь сферичних координат збігається з віссю обертання Землі;

2.     поперечні проекції ( transverse projections, transverse aspect (or case) of a map projections), у яких вісь сферичних координат лежить у площині Екватора;

3.     косі проекції (англ. oblique aspect (or case) of a map projections), коли вісь сферичних координат розташована під кутом до земної вісі.

За способом побудови проекції (за способом отримання) поділяються на: циліндричні, конічні, багатогранні, перспективні.

•         В циліндричних проекціях поверхня сфери проектується на поверхню циліндра.

•         В конічних проекціях поверхня сфери проектується на поверхню конуса.

•         Багатогранні проекції – площини, які відображають сферичні трапеції Землі, що обмежені меридіанами і паралелями. Площина по відношенню до сферичної трапеції може бути дотичною до середньої точки або проходити через вершини кутів трапеції. В результаті проектування сфероїд перетворюється в багатогранник.

•         В перспективних проекціях точки сфери проектуються на площину по прямим лініям.

Залежно від того як розташована площина, на яку проектуються точки земної поверхні розрізняють азимутальні, екваторіальні, горизонтальні проекції. Якщо площина, на яку проектується поверхня еліпсоїда, є дотичною до полюсу, то така проекція називається азимутальною. Якщо площина розташована по дотичній до екватора і паралельно осі обертання Землі, проекція називається екваторіальною. Горизонтальною називається проекція, якщо площа розташовується паралельно горизонту.

Перспективні проекції поділяють також за місцем розташування точки, з якої виходять промені проектування. Якщо джерело вихідних променів знаходяться в центрі проміжного глобуса, то проекції називаються центральними, якщо – на поверхні глобуса – стереографічними, на нескінченно великій відстані – ортографічними.

За виглядом меридіанів та паралелей сітки нормальних проекцій поділяють:

циліндричні проекції, в яких меридіани зображені рівновіддаленими паралельними прямими, а паралелі - прямими, перпендикулярними до них;

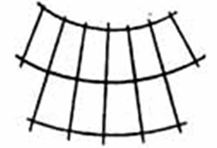конічні проекції з прямими меридіанами, що виходять з однієї точки, і паралелями, що представлені дугами концентричних кіл;

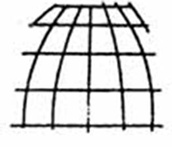азимутальні проекції, в яких паралелі зображуються концентричними колами, а меридіани - радіусами, проведеними із загального центру цих кіл;

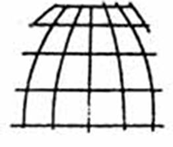псевдоциліндричні проекції, де паралелі представлені паралельними прямими, а меридіани - у вигляді кривих, що збільшують свою кривизну по мірі віддалення від прямого центрального меридіана;

псевдоконічні проекції, в яких паралелі представлені дугами концентричних кіл, середній меридіан - прямою, а інші меридіани - кривими;

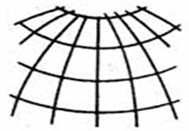поліконічні проекції, в яких паралелі зображені ексцентричними колами, центри яких лежать на прямому центральному меридіані, а всі інші меридіани представлені кривими лініями, які збільшують кривизну з віддаленням від центрального меридіана;

умовні проекції, у яких меридіани та паралелі можуть мати і найрізноманітнішу форму.

Комп'ютерні технології дозволяють розраховувати картографічні проекції будь-якого вигляду із заздалегідь заданим розподілом спотворень. Далі буде спеціально розглянута проблема змішування різних проекцій всередині однієї геоінформаційної системи, особливо при введенні даних.

При виборі картографічної проекції керуються рядом практичних правил.

Якщо аналіз потребує відстеження руху або зміни напрямків руху об'єктів, то найбільш зручними будуть конформні проекції. Цей вид проекцій також найбільше підходить для виробництва навігаційних карт і тоді, коли важливою є кутова орієнтація, як це часто буває з метеорологічними або топографічними даними. Зазначений вид проекцій містить проекції: Меркатора, поперечну Меркатора, конічну конформну Ламберта і конічну стереографічну.

Рівновеликі проекції є найбільш зручними, коли при аналізі переважають розрахунки площ, наприклад при обчисленні зміни співвідношень різних видів рослинності, тощо. Розглядаючи застосування рівновеликих проекцій, слід враховувати розмір території, яка досліджується, а також величину і розподіл кутових спотворень. Невеликі ділянки відображаються із значно меншими кутовими спотвореннями при використанні рівновеликих проекцій, що може бути корисним, коли для аналізу важливими є і площі і форми. З іншого боку, чим більшою є площа досліджуваної території, тим більш точними є вимірювання цієї площі при використанні рівновеликої проекції у порівнянні з проекціями інших типів. Для середньомасштабних карт найчастіше застосовується рівновелика проекція Альберта і рівновелика проекція Ламберта.

Визначення найкоротших маршрутів, особливо для значних відстаней, потребують азимутальних проекцій, оскільки у них є можливим зображення великих кіл як прямих ліній. Такі проекції найчастіше використовуються на картах повітряного сполучення, радіопеленгації, стеження за супутниками, для картографування інших небесних тіл тощо. Азимутальні проекції стали популярними відносно недавно, але їх використання буде зростати разом із зростанням використання ГІС у зазначених областях. Найбільш часто зустрічаються такі азимутальні проекції, як рівновелика Ламберта, стереографічна, азимутальна еквідистантна, ортографічна і гномонічна проекції.

Не варто запам’ятовувати всі назви проекцій, має бути розуміння що всі їх є багато видів і вони мають своє призначення. Треба розуміти, що як і  географічні референц-системи координат, науковці створили геодезичні системи координат, такі як Pulkovo (1942), UTM, UPS тощо. І кожна з них є результатом комбінацій різних проекцій. Для переважної більшості систем координат на площині рівнокутного ефекту намагаються досягнути за допомогою застосування тільки комформних проекцій, найчастіше поперечної Меркатора, полярної стереографічної і конічної комформної Ламберта, а для області поблизу екватора, - проекція Меркатора.

Геодезична система координат називається картографічною (або плановою) системою прямокутних (або плоских) координат. Розглянемо основні системи координат, які застосовуватиме в роботі.

Спроектована система координат Pulkovo (1942) на основі сфероїда має постійні довжини, кути та площі на плоскій двовимірній поверхні. На спроектованій поверхні місцеположення визначаються координатами Х і У на сітці з початком координат у центрі сітки. Чотири  квадранти являють собою можливі комбінації позитивних і негативних координат Х і У.

Найбільш широко розповсюдженою у ГІС системою проецій та координат є універсальна поперечна Меркатора (universal transverse Mercator (UTM)). UTM ділить земну поверхню на 60 пронумерованих вертикальних  зон шириною по 6°, кожна з яких проходить від 80° південної широти до 84° північної широти.

УСК-2000 (англ. UCS-2000) — Державна геодезична референцна система координат України, яку використовують для виконання топографо-геодезичних та картографічних робіт.

Можна в ГІС системах виконувати також і перехід між системами координат. Існує різниця між проекцією з якою працює користувач і проекцією вихідної карти. Для дрібномасштабних карт ця різниця значна. Для виконання вірної трансформації  картографічних даних з однієї проекції в іншу потребують знань про проекції джерела даних і похідної проекції. Можна звичайно використати проміжний етап перетворення спершу прямокутних координат в географічні, а потім в потрібну проекцію прямокутних координат.

Не обравши жодної системи під час створення шарів просторових даних або працюючи з даними з різних систем координат, ми маємо розуміти причину чому на екрані ми не бачимо того результату, на який очікуємо. Чому об’єкти різних шарів не накладаються а знаходяться в різних місцях. Чому вони не відображаються на екрані. Чому не можемо встановити масштаб обєктів тощо.