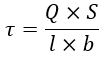Тема 2. Основи розрахунку металевих конструкцій. Розрахунок на стиск і згин

Центрально стиснуті, як і центрально розтягнуті елементи, – це такі елементи, напрямок дії зусилля в яких співпадає з поздовжньою віссю елемента.

Центрально стиснуті елементи поділяють на короткі і довгі гнучкі. Короткі – це елементи, довжина яких перевищує найменший поперечний розмір не більш, як в 5 разів. Довгі – відповідно більш, ніж в 5 разів.

Центрально стиснуті стержні розраховуються за І групою граничних станів. Їх несуча здатність може бути вичерпана внаслідок настання одного з двох граничних станів:

• втрати міцності, коли руйнується матеріал елемента (для коротких стержнів);
• втрати стійкості, коли порушується прямолінійна форма елемента без механічних пошкоджень матеріалу (для довгих стержнів).

Короткі стиснуті стержні, як і розтягнуті, розраховуються на міцність за формулою:

де N – розрахункове осьове зусилля;
A_n – площа перерізу “нетто”;
R_y – розрахунковий опір за межею текучості;
γ_с – коефіцієнт умов роботи;
γ_n - коефіцієнт надійності за відповідальністю.

В будівельній практиці короткі стержні зустрічаються надзвичайно рідко, і в основному ми маємо справу з довгими стержнями, несуча здатність яких обмежується не внаслідок втрати міцності, а в результаті втрати стійкості.

Довгі стиснуті стержні розраховуються за умовою стійкості.

Проблема стійкості стальних конструкцій має виключно важливе значення – біля 40% аварій МК виникає внаслідок її недооцінки.

Суть проблеми стійкості полягає в наступному.

Якщо пружний стержень стискувати центрально прикладеною силою N, то, доки сила мала, прямолінійна форма рівноваги стійка. Якщо навіть відхилити стержень від положення рівноваги невеликою боковою силою, то після її зняття стержень відновить свою прямолінійну форму.

При зростанні сили N наступить момент, коли робота, що здійснюється силою при пружному переміщенні Δ, перевищить потенційну енергію пружної деформації стержня, і прямолінійний стан стає нестійким. Поряд із стиском з’являється нова форма деформації – згин (рис. 1).

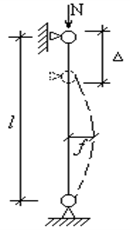
Поздовжня сила, яка відповідає моменту переходу стержня із прямолінійного в криволінійний стан рівноваги, називається критичною силою N_сг.

Згин, який виникає від дії центрально прикладеної поздовжньої сили, називається поздовжнім згином.

l_ef – розрахункова довжина стержня. Вона характеризує не тільки його протяжність, але й форму, яку приймає стержень при втраті стійкості:

l_ef = μ · l;
μ - коефіцієнт приведення розрахункової довжини, який залежить від умов закріплення кінців стержня;
l - геометрична довжина стержня, рівна найменшій відстані між точками закріплення стержня від поперечного зміщення.

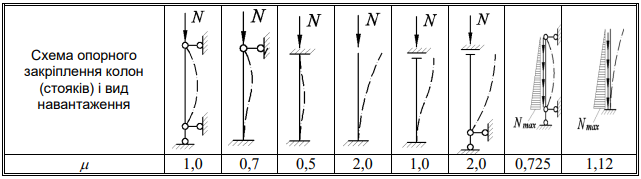
З рисунка видно, що стержні, які мають однакову геометричну довжину, будуть мати різні розрахункові довжини.

Умова стійкості центрально стиснутого елемента:

де φ – коефіцієнт стійкості при центральному стиску.

Коефіцієнт φ залежить від гнучкості та розрахункового опору сталі.

Розрахунок розтягнутих і стиснутих елементів виконують тільки за І гр. граничних станів.

Розрахунок згинальних елементів виконують за двома групами граничних станів:

• за І групою - розрахунок на міцність за максимальними нормальними, максимальними дотичними, місцевими і зведеними напруженнями, розрахунок загальної та місцевої стійкості;
• за ІІ групою - розрахунок на жорсткість (за прогинами).

Граничний стан за втратою міцності розглядають для двох розрахункових випадків:

1. При роботі матеріалу в межах пружності;
2. З врахуванням розвитку обмежених пластичних деформацій.

Крім цього згин може бути в одній площині (прямий згин) або в двох взаємно перпендикулярних площинах (косий згин).

Найбільш типовим прикладом елементів, що згинаються, є балка, на яку одночасно діють згинальні моменти М та поперечні сили Q.

Згинальні моменти зумовлюють виникнення в поперечних перерізах нормальних напружень:

а поперечні сили – дотичних:

де 𝑦 – відстань від центра ваги перерізу до шару волокон, у яких визначають нормальні напруження;
І – момент інерції перерізу відносно головної центральної осі, перпендикулярної до площини дії моменту;
S - статичний момент;
b – ширина чи товщина перерізу.

Умова міцності при дії нормальних і дотичних напружень: