Чисельне рішення оптимізаційних задач

Для рішення цієї задачі використовуються методи золотого перетину або параболічної інтерполяції (у залежності від форми задання функції), реалізовані в програмі fminbnd.

Приклад.

Знайти мінімальне значення функції:

f(x) = 24 – 2x /3 + x^2/30   на [5; 20].

Будуємо графік цієї функції, щоб переконатися в наявності мінімуму на заданому інтервалі.

Протокол програми

>> x = 5.0 : 0.001:20.0 ;    y=24-2*x/3+x.^2/30;

>> рlot(x, y) ; grid on

З'являється вікно з графіком цієї функції (рис. 4.1), де відзначаємо наявність мінімуму.

Далі, для точного визначення координати і значення мінімуму використаємо функцію fminbnd:

>> [x, y] = fminbnd ( ¢ (24.0 – 2* x/3 + x,^2/30) ¢, 5.0, 20.0)

Результат пошуку

х =

       10.0000

у =

       20.6667

>> hold on; gtext ( ¢Minimum¢)

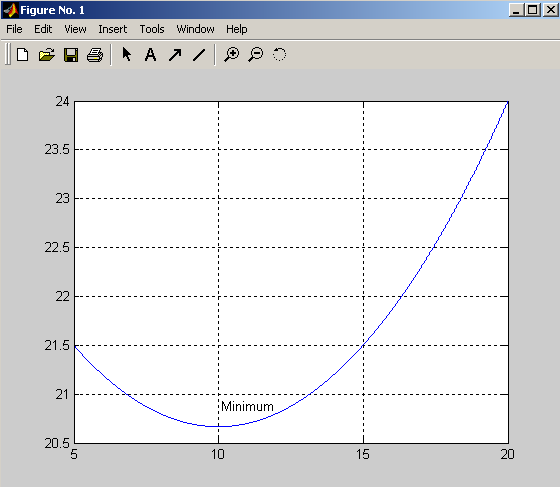
Рис. 4.1. Мінімальне значення функції f(x) = 24 – 2x /3 + x^2/30