Тема 3. Концептуальніо-наукові засади математичного моделювання бізнес=проєктів

У сільському господарстві взаємозв’язки в економічних процесах характеризують перетворення виробничих ресурсів в готову продукцію. Для вивчення процесів управління ефективною організацією цих перетворень створюються моделі, до яких застосовують методи мислення по аналогії. Таким чином, модель є загально методологічне наукове поняття, яке застосовують в різних галузях науки і техніки. Вона має важливе значення для дослідження економічних проблем при необхідності глибокого проникнення у специфічність об’єктів, що вивчаються. Між моделлю і досліджуваним економічним процесом, повинно означати сходність, а не їх тотожність. Модель, відтворюючи реальний економічний процес, спрощує його, відволікається від ряду його непринципових рис. Тому модель – це умовний образ, який абстрактно відображає основні взаємозв’язки, які існують в реальному економічному процесі. В моделях відбувається абстрагування не тільки від несуттєвих зв’язків, але і від якості предметів і конкретного значення величин. Всі суттєві характеристики і властивості об’єкту чи процесу, що вивчається записуються за допомогою алгебраїчних формул, частіше за все, це рівняння або нерівності. Запис всіх характеристик і властивостей економічного процесу у вигляді алгебраїчних формул називають економіко-математичною моделлю. Таким чином, під структурною економіко-математичною моделлю слід розуміти концентрований вираз суттєвих зв’язків і закономірностей процесу функціонування економічної системи в математичній формі.

При кібернетичному тлумаченні економіко-математичної моделі умови задач, що вирішуються, будуть представляти собою вхідну інформацію або параметри управління. Зміни цих параметрів, в процесі вирішення задачі, будуть характеризувати зміну стану досліджуваного об’єкту, а екстремум цільової функції буде являтись критеріальним показником досягнення системою оптимального стану. В економіко-математичних моделях параметри зазвичай надаються у вигляді таблиць чисел, які пов’язані в єдину систему функціональних рівнянь різного типу.

Найбільш поширеними в практиці досліджень є економіко-математичні моделі, які представлені балансовими і оптимізаційними моделями. Балансові, як правило, характеризуються системою балансових таблиць, які мають форму шахового балансу і можуть бути записані у вигляді квадратної матриці. Оптимізаційні моделі відрізняються від балансових тим, що метою їх побудови є не стільки описування структури економічної системи, скільки математичне описування умов її функціонування. Якщо перші моделі, в основному, повинні задіяти звітний матеріал, то оптимізаційні широко використовують планово-нормативну інформацію.

Моделі розробляють структурні і розширені. В структурній моделі зв’язки і закономірності економічної системи інтерпретують в математичній формі. Розширена економіко-математична модель містить звітний і планово-нормативний матеріал, який описує умови функціонування економічної системи. Така модель оформляється у вигляді матриці.

Економіко-статистичні моделі представляють собою кореляційне рівняння зв’язку залежної змінної величини (Y) і однією або декількох незалежних змінних величин (факторів) Хі. За допомогою таких рівнянь визначають кількісну міру впливу факторів (Xі) на результативний показник (Y). За допомогою робочого рівняння визначають теоретичні або прогнозні значення результативного показника, та проводять факторний аналіз відповідного показника.

Як приклад економічної моделі розгляньмо спрощений (ідеалізований) варіант так званої «павутиноподібної моделі», яка описує процес формування попиту і пропозиції певного товару чи виду послуг на конкурентному ринку (випадок досконалої конкуренції). Ідеться про формалізацію економічного закону попиту та пропозиції, згідно з яким: кількість товару, що його можна продати на ринку (тобто попит), змінюється у напрямку, протилежному зміні ціни товару; кількість товару, який виробляють і доставляють на ринок (тобто пропозиція), змінюється у тому самому напрямку, що й ціна; водночас реальна ринкова ціна формується на рівні, на якому попит і пропозиція наближено дорівнюють одне одному (приблизно збігаються з деякою заданою точністю), тобто перебувають у рівновазі.

Першим, хто спробував математично сформулювати цей закон, був французький учений А. Курно. Подамо математичну формалізацію положень цього закону. Нехай Xt — ціна товару в момент часу t, а Dt і St — кількість товару, купленого і пропонованого відповідно на ринку в той самий момент часу t. Тоді, з урахуванням одного інтервалу часу, необхідного виробникам-продавцям для того, щоб «зреагувати» на ціну X, можна математично сформулювати наведені закономірності:

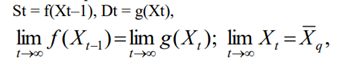
де f(X) — деяка монотонно зростаюча і g(X) — монотонно спадна функції від аргумента X (тобто від ціни), Xq — рівноважна ціна.

Математичні співвідношення, що відображають закон попиту і пропозиції, можуть бути проілюстровані. Як бачимо на рис. 1.2, процес формування рівноважної ціни почався з призначення в перший (початковий) момент часу ціни на рівні X1. Продовження цього процесу (індексовано стрілками) павутиноподібно прямує до точки перетину кривих g(X) і f(X).

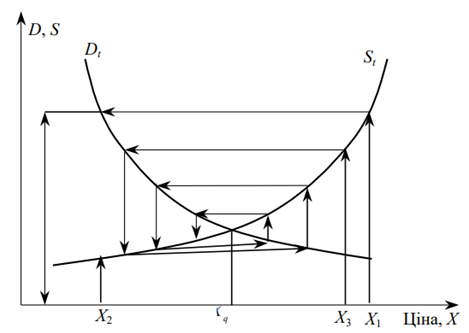
Рис. 3.3. Графік процесу формування попиту і пропозиції

Реальна модель закону попиту і пропозиції, звичайно, складніша. Зокрема, D і S залежать не лише від ціни X. Крім цього, зв’язок (наближений) між D і S, з одного боку, і ціною X — з другого, має не детермінований, а стохастичний характер. Щоб описана вище модель з економічної перетворилася в економетричну, потрібно вести мову не взагалі про закон попиту і пропозиції, а про конкретну дію його в даному секторі економіки в певний час і стосовно конкретного товару (чи виду послуг). Відповідно, конкретизація виду функцій g(X) і f(X), повинна проводитися на підставі статистичних даних щодо значень Xt, St, Dt, де tÎ{1,...,T}, Т — кількість періодів, протягом яких здійснювався моніторинг і отримані дані.

Приклад «Павутиноподібної моделі» фірми

Підприємець збирається вкласти кошти у створення фірми, яка випускатиме товар і реалізовуватиме його на ринку. Його цікавить, як буде поводити себе ціна товару за змін обсягів виробництва. Він розуміє, що при збільшенні обсягів виробництва ціна одиниці товару спадатиме. Йому важливо знати, за яких умов ціна буде стабільною. У науковій літературі описано кілька варіантів відповідної моделі. У них приймається низка гіпотез, зазвичай припускається, що попит на деякий продукт упродовж певного (заданого) проміжку часу залежить від ціни (та інших чинників) на цьому проміжку. Що стосується пропозиції, то вона визначається цінами попереднього проміжку часу (тиждень, місяць, квартал тощо). Окрім цього, приймається гіпотеза, згідно з якою ринок перебуває в умовах локальної рівноваги. Як уже зазначалось, історично така модель отримала назву «павутиноподібної».

Аналіз і розв’язання

Існують як мінімум чотири варіанти відповідної моделі: детермінована, стохастична, модель з навчанням та модель із запасами. У детермінованій моделі відсутнє урахування випадкових чинників. У стохастичній моделі враховується вплив на попит непередбачуваних коливань уподобань і доходів споживачів, а також інших випадкових чинників, які впливають на попит. Пропозиція на попередньому проміжку часу також вважається залежною від впливу випадкових чинників, усі вони відображають вплив коливань у технологічному процесі тощо. Умова локальної рівноваги означає збіг (незначну різницю) попиту і пропозиції з точністю до певної заданої величини.

У моделі з навчанням приймається гіпотеза, за якою постачальники (виробники), ураховуючи тенденцію зміни цін, планують випуск продукції на наступний проміжок часу. В останніх двох моделях ціни встановлюються на такому рівні, щоб забезпечити локальну рівновагу лише за рахунок поточного виробництва, і жодних запасів продукції не створюється (зокрема, тому що продукція швидко псується). У модель із запасами вводиться додаткова група учасників ринкового механізму, котрих можна назвати комерсантами. Вони тримають запаси та організовують торгівлю.

Приклад стохастичної моделі.

Припустимо, що попит на t-му проміжку часу лінійно залежить від поточної ціни (це припущення не є обов’язковим. Навпаки, воно досить жорстке. У реальних процесах припускається, що така залежність буде нелінійною. Вид залежності визначається на підставі застосування економетричних методів і моделей). Окрім цього, вважатимемо, що попит на ринку має випадковий розкид. Для формалізованого опису необхідно в наших припущеннях обчислити на підставі доступної інформації відповідно оцінки коефіцієнтів лінійного рівняння та похибку як випадкову величину, що має певний закон розподілу. У результаті відповідних обчислень можна отримати, зокрема, такий вираз:

Dt = A – BXt + ut,

де Dt — попит на t-му проміжку часу; A, B — коефіцієнти лінійної регресії (В > 0); Xt — ціна одиниці продукції на t-му проміжку часу; ut — випадкова величина, що має заданий закон розподілу.

Логічно припускати, що попит симетрично коливається відносно деякого середнього значення, котре визначається постійними коефіцієнтами лінійного рівняння (їхніми оцінками). Тому, зокрема, можна обрати нормальний закон розподілу з нульовим математичним сподіванням і заданим середньоквадратичним відхиленням su.

Припустимо, що пропозиція впродовж поточного проміжку часу також лінійно (в середньому) залежить від ціни, але не поточної, а такої, що являє собою комбінацію цін на двох попередніх проміжках часу. У найпростішому випадку це може бути середнє значення цін протягом двох попередніх проміжків часу. Отже, для обчислень пропозиції можна (якщо для цього є підстави) використовувати таку залежність:

St = C + KX(r) + vt ,

де St — пропозиція впродовж t-го проміжку часу; C, K — коефіцієнти лінійної регресії (K > 0); X(r) — середнє (середньозважене) значення ціни на двох попередніх проміжках часу; vt — випадкова величина, що має заданий закон розподілу.

Можна, зокрема, для спрощення обрати нормальний закон розподілу випадкової величини vt з нульовим математичним сподіванням і заданим середньоквадратичним відхиленням sv. Ціна X(r) може визначатися згідно з формулою:

X(r) = Xt–1 – r(Xt–1 – Xt–2),

де Xt–1 — ціна на (t – 1)-му проміжку часу; Xt–2 — ціна на (t – 2)-му проміжку часу; r — ваговий коефіцієнт, значення котрого задається в моделі в діапазоні (0 £ r £ 1).

Якщо r = 0, то середньозважена ціна X(r) = Xt–1. Це означає, що навчання в модель не закладене. Для другого граничного випадку (r = 1) середньозважена ціна X(r) = Xt–2. Це також означає, що навчання у моделі відсутнє, але для визначення пропозиції використовується віддалене в часі значення ціни. За умови r = 0,5 середньозважена ціна X(r) дорівнює середньоарифметичному значенню цін Xt–1 та Xt–2.

До моделі треба ще долучити рівняння локальної рівноваги ринку:

St = Dt + wt,

де St — пропозиція на t-му проміжку часу; Dt — попит на t-му проміжку часу; wt — випадкова величина, котра має заданий закон розподілу.

Можна прийняти гіпотезу, що wt має нормальний закон розподілу з нульовим значенням величини математичного сподівання та із середньоквадратичним відхиленням — sw. Система рівнянь (1.1)—(1.4) після відповідних простих перетворень зводиться до такого виразу:

Xt = F(Xt–1, Xt–2),

де F(Xt–1, Xt–2) — функція, що є оцінкою кореляційно-регресійного зв’язку між змінними Xt, Xt–1, Xt–2.

Спочатку необхідно якимось наближеним способом визначити ціну для перших двох проміжків часу. Після цього можна проводити обчислення згідно з виразом (1.5) певну кількість разів (ітерацій). Результати обчислень можуть бути подані також у графічному вигляді. Задача аналізу полягає у дослідженні впливу параметрів системи на характер залежності ціни у часі (як функції часу), а також у знаходженні рівноважної ціни.