Тема 2. Метод скінченних елементів. Математичні основи методу скінченних елементів

озглянемо тепер СЕ у складі рами, розташований під кутом α до осі X в глобальній системі осей координат. Необхідно перейти від матриці реакцій [r]_j в локальній системі координат до матриці [r]_j у глобальній системі координат.

Задачу вирішуємо таким чином. На початку побудуємо матрицю [c]_j, яка перетворить переміщення СЕ {Z}_j в глобальній системі координат в переміщення {V}_j:

                          {V}j= [c]j. {Z}j                                (3.6)

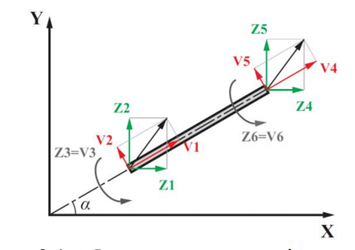
Рисунок 3.1 - Формування матриці перетворень

З рисунку 3.1 запишемо рівняння:

V1 = Z1*cosα+Z2*sinα

V2 = -Z1*sinα+Z2*cosα

V3 = Z3

V4 = Z4*cosα+Z5*sinα

V5 = -Z4*sinα+Z5*cosα

V6= Z6

У матричній формі приведений вище запис матиме вигляд:

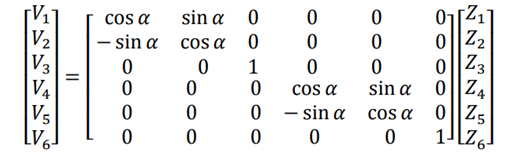(3.7)

чи у блочній формі

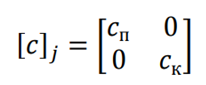
Оскільки ми розглядаємо плоскі пружні системи, то вектори вузлових зусиль і вузлових переміщень, як для окремого елементу, так і для споруди в цілому, пов’язані між собою лінійно:

- в локальній системі координат

                         {S}j'=[r]j' * {V}j                       (3.8)

- в глобальній системі координат (основне рівняння МСЕ)

                          {S}j=[r]j * {Z}j                              (3.9)

Крім того,

                          {V}j=[c]j * {Z}j                            (3.10)

Аналогічно

                               {S}'_j=[c]_j.{S}_j                            (3.11)

де {S}'_j,{S}_j  - вузлові зусилля СЕ відповідно в локальній і глобальній системах координат.

Тоді

{S}_j = [c]_j^-1 *{S}_j' = [c]j^-1 * [r]j'  {V}_j=[c]j^-1* [r]j'  * [c]j  {Z}j

Для матриці направляючих косинусів виконується рівність [c]j^-1= [c]j^T. Тоді

{S}j=[c]j^T  * [r]j' *  [c]j * {Z}j

Позначимо

                            [r]_j =[c]_j^T  [r]_j' * c]_j                                         (3.12)

Вираз (3.12) і є формулою для обчислення матриці жорсткості СЕ в глобальній системі координат.

При формуванні матриць жорсткості окремих елементів  [r]_j, мають бути зафіксовані початок і кінець кожного стержня, оскільки від цього залежить знак кута а, що визначає орієнтацію стержня в глобальній системі координат XOY.