Лекція 1.3 MATLAB у задачах прикладної математики

Одним із розповсюджених і практично важливих випадків зв'язку між аргументом і функцією є задання цього зв'язку у виді деякої таблиці {x_i ; y_i}, наприклад, експериментальні дані. На практиці часто доводиться використовувати табличні дані для наближеного обчислення y при будь-якому значенні аргументу х (з деякої області).

Цій меті служить задача про наближення (апроксимації) функцій: функцію f(x) потрібно приблизно замінити деякою функцією g(х) так, щоб відхилення g(х) від f(x) у заданій області було найменшим. Функція g(х) при цьому називається апроксимуючої. Якщо наближення будується на заданій дискретній множині {x_i}, то апроксимація називається дискретною. До неї відносяться інтерполяція, середньоквадратичне наближення тощо.

При побудові наближення на безперервній множині (наприклад, на відрізку [a, b]) апроксимація називається безперервною або інтегральною.

MATLAB має засоби дискретної та безперервної апроксимації з візуалізацією результату.

Розглянемо дискретну апроксимацію (обробка експериментальних даних).

Приклад.

Використовуючи лінійну і поліноміальну апроксимації, одержати емпіричні формули для функції y=f(x), заданої в табличному виді:

Оцінити погрішність емпіричних формул.

Протокол програми. У вікні команд набираються значення x_i і y_i. Далі виконується команда побудови графіка тільки вузлових точок.

>> x = [0.75, 1.50, 2.25, 3.00, 3.75] ;

>> y = [2.50, 1.20, 1.12, 2.25, 4.28] ;

>> рlot (x, y, ¢ о ¢) ;

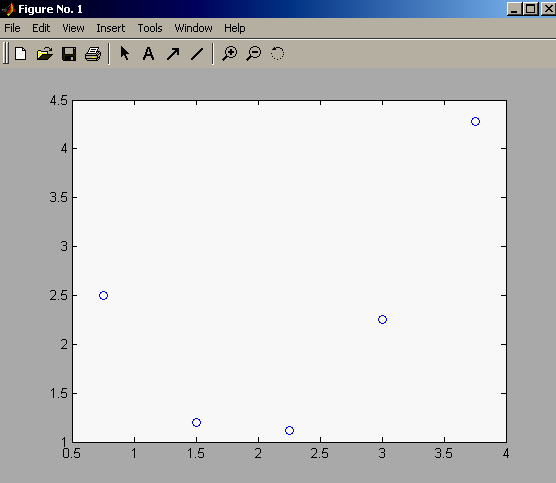 Рис. 3.1. Вузлові точки

Увага. Варто пам'ятати, що при поліноміальній апроксимації максимальний степінь полінома на 1 менше числа експериментальних точок.

На панелі інструментів вікна графіка вузлових точок у меню Tools виконуємо команду Basic Fitting. З’являється вікно Основний Монтаж. У цьому вікні виділяються необхідні дані апроксимації. Зокрема, можна задати наступні операції:

• показати рівняння апроксимуючої функції y = g(х);
• вибрати метод підбору.

У нашій задачі вибираємо лінійну і поліноміальну апроксимації. У вікні графіка з’являються відповідні графіки і формули апроксимуючих функцій (рис. 3.2).

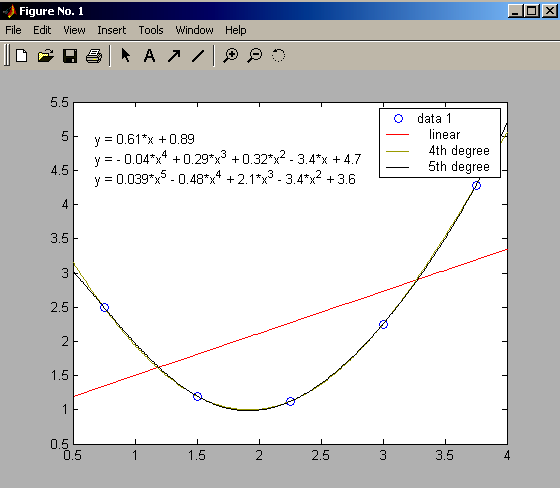
Рис. 3.2. Графіки і формули апроксимуючих функцій

Щоб встановити погрішність апроксимації, треба виділити параметр Графік залишку у вікні Основний Монтаж, і  Показати норму залишків. Графік похибок з нормами можна винести в окреме вікно, або разом із графіком і апроксимуючими функціями – суб-графік.

Норма погрішностей вказує на статистичну оцінку средньоквадратичної похибки. Чим вона менше, тим точніше апроксимуюча функція    y = g(х). У нашому прикладі:

Linear : norm of residuals (норма погрішності) = 2.1061

Quadratic : norm of residuals = 0.10736

Cubic : norm of residuals = 0.035857

4 th degree : norm of residuals = 9.6305e-015.

Графік погрішностей можна виводити у виді діаграм (зони), ліній (лінії) або окремих крапок (фрагменти). Сам графік погрішностей являє собою залежність різниці g(х) - f(x) в умовних точках, з'єднаних прямими лініями.

Крім лінійної і поліноміальної апроксимацій можна вибрати сплайн- апроксимацію – коли на кожнім інтервалі наближення використовується кубічний поліном з новими коефіцієнтами. У цьому випадку не можна одержати вираз для апроксимуючої функції, тобто така апроксимація є неповною.