Лекція 1.3 MATLAB у задачах прикладної математики

Задача знаходження коренів нелінійних рівнянь зустрічається в різних областях науково-технічних досліджень. Проблема формулюється в такий спосіб: нехай задана безперервна функція f(x) і потрібно знайти корінь рівняння

f(x) = 0.

Припустимо, що відомо інтервал зміни х [a; b], на якому необхідно досліджувати функцію f(x) і знайти значення х₀, при якому f(x₀) дорівнює або досить мало відрізняється від нуля.

Дана задача в системі MATLAB може бути вирішена в такий спосіб, Спочатку необхідно побудувати графік функції f(x) на заданому інтервалі і переконатися в існуванні кореня або декількох коренів. Потім застосувати програми пошуку коренів. Якщо існує один корінь і графік f(x) перетинає вісь х, то можна застосувати програму fzero. Якщо f(x) має більше одного кореня х, то варто застосувати більш функціональний оператор fsolve з пакету Optimization Toolbox, що вирішує задачу методом найменших квадратів. Програма fzero використовує відомі чисельні методи: розподіл відрізка навпіл, зворотної квадратичної інтерполяції.

Приклад.

Знайти корінь нелінійного рівняння 10^х + 2х – 100 = 0 на інтервалі [1,0; 2,0].

Протокол програми

>> % Будуємо графік заданої функції

>> x = 1.0 : 0.001:2.0;  y = 10.0.^x + 2.0*x – 100.0;

>> рlot (x, y) ;  grid on

З'являється вікно з графіком функції 10^х + 2х – 100 (рис. 3.4), з якого випливає, що корінь функції на заданому інтервалі існує. Для точного визначення кореня застосовуємо fzero і fsolve.

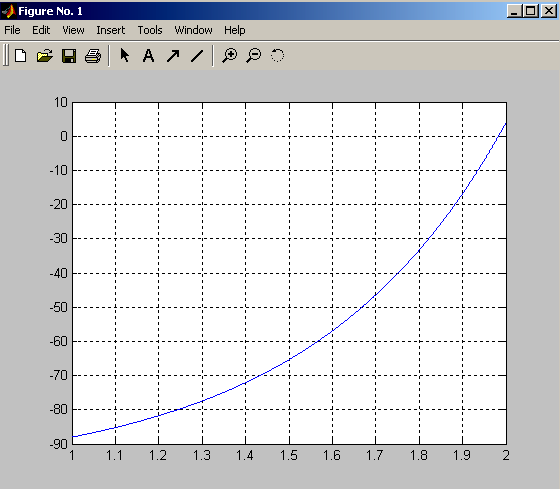
Рис. 3.4. Графік функції 10^х + 2х – 100

>> Х1=fzero('(10.^x+2*x-100)',[1 2])

Результат розв’язку

Х1 =

         1,9824

>> X2 = fsolve ( '(10.^x + 2.0*x - 100.0)', 1:2);

Результат рішення

Х2 =

         1.9824