Тема 5. Принципи розрахунку, покладені в основу обчислювальних комплексів
1. Методи визначення напружено-деформованого стану конструкцій
НДС будівельних конструкцій можна визначити на основі двох рівноцінних напрямків: локального та інтегрального.
Перший базується на розгляді рівнянь будівельної механіки, це рівняння статики, рівняння нерозривності, фізичні та геометричні рівняння. Рівняння локального напрямку подані в таблиці 6.1.
Таблиця 6.1 – Види рівнянь локального методу будівельної механіки
|
Вид рівнянь |
Матричний запис |
Запис з використанням обумовленості про підсумовування Ейнштейна |
|
Статичні (рівняння рівноваги) |
|
де
|
|
Геометричні рівняння нерозривності |
|
де матриці форми; |
|
Фізичні рівняння |
|
де |
Другий напрямок – базується на варіаційному численні, основним поняттям якого є енергія. Енергетичний (термодинамічний) метод вивчення явищ природи розглядає зміни в системі як виділення чи поглинання енергії, перетворення одних видів енергії в інші. Цей метод встановлює загальний напрямок процесів, визначає кінцевий стан, але не дозволяє розглянути протікання процесу.
Енергія – це найбільш загальна кількісна характеристика руху. Внутрішня енергія системи – кількісна форма всіх форм руху, що проявляються при взаємодії внутрішніх елементів системи, утворюючих структуру даного рівня.
В результаті для розв’язання крайових задач із визначення НДС будівельних конструкцій потрібно розв’язувати систему із 15 диференційних рівнянь в частинних похідних з конкретними граничними умовами.
Ця система крайових задач може бути розв’язана числовими методами, оскільки аналітичних розв’язань існує дуже мало:
- методом скінченних різниць (МСР);
- методом скінченних елементів (МСЕ);
- методом граничних елементів (МГЕ).
Дуже багато фізичних явищ зводиться до крайових задач для рівнянь в частинних похідних. Тому область прикладання МСЕ дуже широка. Успішне використання на теперішній час МСЕ пов’язано з таким.
1. Крайові задачі в рівняннях з частинними похідними перетворюються у варіаційні, що дозволяє в рамках прийнятої апроксимації відшукати оптимальне рішення.
2. ЕОМ дозволяє розв’язувати СЛАР високих порядків, а саме до них зводиться пошук розв’язків крайових задач.
3. Стало можливим використання універсальних програм, скрупульозно складених спеціалістами, що дозволяє користувачеві при виконанні великого обсягу розрахунків обмежитись лише підстановкою вхідних даних.
Шрифти
Розмір шрифта
Колір тексту
Колір тла
Кернінг шрифтів
Видимість картинок
Інтервал між літерами
Висота рядка
Виділити посилання
Вирівнювання тексту
Ширина абзацу

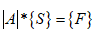
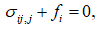 (6.1)
(6.1)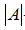
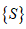 – вектор шуканих зусиль;
– вектор шуканих зусиль; 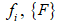 – вектор
зовнішніх навантажень.
– вектор
зовнішніх навантажень.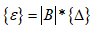
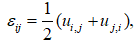 (6.2)
(6.2)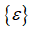 –вектор деформацій;
–вектор деформацій; 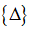 – вектор переміщень;
– вектор переміщень; 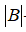 – матриця градієнтів, похідна від
– матриця градієнтів, похідна від 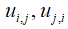 – похідні від переміщень.
– похідні від переміщень.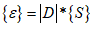
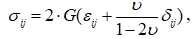 (6.3)
(6.3)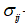 – тензор напружень;
– тензор напружень;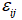 – тензор деформації;
– тензор деформації;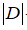 – матриця піддатливості;
– матриця піддатливості;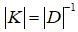 – матриця
жорсткості;
– матриця
жорсткості;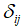 – дельта Кронекера.
– дельта Кронекера.