Тема 9. Розрахунки з врахуванням фізичної нелінійності
1. Фізична нелінійність бетону.
Відхилення від закону Гука спостерігається для бетону вже на початкових стадіях навантаження. У бетоні як в матеріалі пружно-пластичному має місце нелінійна залежність між напруженнями і деформаціями, тобто при виконанні розрахунку стає необхідним врахування фізичної нелінійності бетону
σ = f(ε) (9.1)
Початковий модуль пружності бетону Е0 відповідає лише миттєвому навантаженню зразка, при якому виникають тільки пружні деформації.
Геометрично Е0 виражається тангенсом кута нахилу прямої пружних деформацій (рис. 9.1).
Рисунок 9.1 – Залежність σ-ε для бетону і модуль деформацій
При тривалій дії навантаження у зв’язку з розвитком пластичних деформацій модуль повних деформацій бетону стає змінною величиною і геометрично може бути виражений тангенсом кута нахилу дотичної до кривої σ-ε в точці із заданим напруженням:
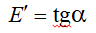(9.2)
Отже, модуль деформації бетону Е’ є похідною від напруження по деформаціях
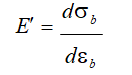(9.3)
Користуючись змінним модулем деформації Е’, можна було б знаходити деформації інтегруванням функції
але практично
такий спосіб визначення
деформації важкий, оскільки
тут потрібна аналітична залежність 
За пропозицією В. І. Мурашева, при розрахунку залізобетонних конструкцій користуються середнім модулем пружнопластичності бетону, що є тангенсом кута нахилу січної до кривої повних деформацій в точці із заданим напруженням (див. рис. 9.1):
(9.4)
В файлах звітів після виконання нелінійного розрахунку друкуються переміщення та зусилля у вузлах та елементах схеми, а також виводяться повідомлення:
- про розвиток процесу тріщиноутворення з орієнтацією тріщин в загальній системі координат при переважанні розтягуючих напружень;
- про дроблення матеріалу, при переважанні стискуючих напружень;
- про виколювання матеріалу між тріщинами при знакозмінних напруженнях;
- про текучість, розриви, зім’яття, зрізи арматури;
- про точки утворення пластичних шарнірів.
Шрифти
Розмір шрифта
Колір тексту
Колір тла